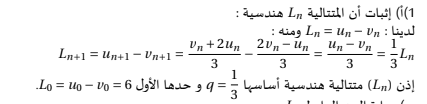الاسئلة الشائعة في البكالوريا
المتتاليات العددية 2) الاحتمالات 1) الدوال
الاعداد المركبة 5) الهندسة في الفضاء 4) صح وخطأ
7) التكامل والدوال الاصلية


**اضغط هنا البرهان بالتراجع تمارين محلولة**
**حساب الحدود**
*مثال*
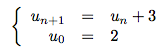
حساب الحدود الاولى
u1 = u0 + 3 = 2 + 3 = 5
u2 = u1 + 3 = 5 + 3 = 8
u3 = u2 + 3 = 8 + 3 = 11
u4 = u3 + 3 = 11 + 3 = 14
**المتتالية الهندسية**
مثال*1*
نضع
u0 = 2
(n ∈ N), vn = 2un - 1 و un+1 = 3un - 1
أثبت أن(`v_n `) متتالية هندسية
حساب vn+1
vn+1 = 2un+1 - 1
vn+1 = 2 × (3un - 1) - 1
vn+1 = 6un - 2 - 1
vn+1 = 6un - 3
vn+1 = 3(2un - 1)
vn+1 = 3vn
ومنه (`v_n `) متتالية هندسية أساسها 3 وحدها لاول3
الحد الاولv0 = 2u0 - 1 = 2 × 2 - 1 = 3
مثال*2*
vn = un² - 4 و 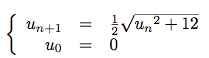
أثبت أن(`v_n `) متتالية هندسية
**الحل**
حساب `v_(n+1) `
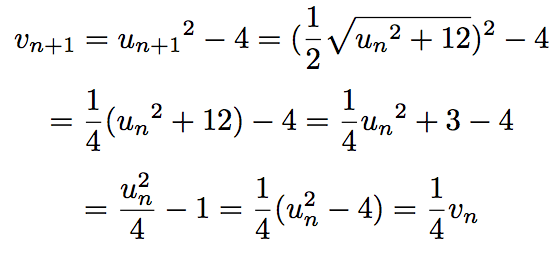
`v_(n+1)=1/4 v_n `
ومنه `v_n ` متتالية هندسية أساسها `1/4 ` وحدها لاول-4
*تمثيل الحدود*
*مثال*
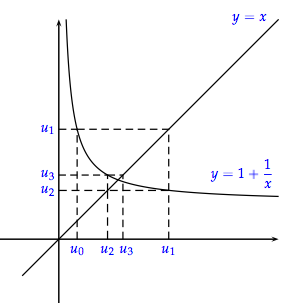
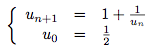
اولا نرسم المنحنى 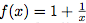 مع المستقيم ذو المعادلةة `y=x `
مع المستقيم ذو المعادلةة `y=x `
ثم نعين الحد الاول المعطى على محور الفواصل ثم ننتقل الى المنحنى ثم المستقيم ثم ننزل الى محور الفواصل لنتحصل على الحد المولي
``كما هو موضح في الرسم
**التمرين الاول**لتكن (vn ) متتالبة حسابية حيث
v3=3 و v6=24.
- أحسب v0 والاساس.
- نفس الاسئلة اذا كانت المتتلية هندسية
* v3=v0+3rو v6=v0+6r. v0=2v3−v6=6−24=−18,
- r=(v3−v0)/3=21/3=7.
- اذن r=7 ** v3=v0×r3وv6=v0×r6. v0=v23v6=38,
- r3=v3v0=3×83=8
- اذن r=2.
**التمرين الثاني**لتكن (un) متتالية معرفة كمايليu0=3وun+1=4un−2un+1.من أجل x≠−1, نضع f(x)=4x−2x+1.
- أدرس تغيرات f على [1,+∞[.
- بين أنه من أجل كل n≥0, فان un>1.
- لتكن المتتالية (vn) ( n∈N ),vn=un−2un−1.بين أن (vn) نتتالية هندسية
- اكتب عبارة الحد العام un بدلالة n.
- بين أن (un) متقاربة ثم أحسي نهايتها
* من أجل x≠-1
f′(x)=6(x+1)2>0. f مترايدة تماما [1,+∞[.
اثبات انها متتالية هندسية
- vn+1=4un−2un+1−24un−2un+1−1=4un−2−2un−24un−2−un−1=2un−43un−2=23(un−2un−1)=23vn.ادن عبارة الحد العام,vn=(23)nv0=12(23)n.
un−2un−1=vn⟺un−2=unvn−vn⟺un(1−vn)=2−vn⟺un=2−vn1−vnوعليهun=2−12(23)n1−12(23)n. (2/3)n تؤول الى 0, اذن (un) متقاربة 2.
متتالية معرفة كما يلي u0∈]0,1] un+1=un2+u2n4.
- بين أن 0<un≤1.
- أثبت أن المتتالية رتيبة.
- استنتج انها متقاربة ثم أحسب نهايتها
البرهان بالتراجع يترك لكم*
دراسة الاتجاه التغيرات المتتالية*- un+1−un=u2n4−un2=un4(un−2)لدينا un>0 و un−2≤−1<0. ادن un+1−un<0. المتتالية (un)n≥0 متناقصة تماما
بما أن المتتالية متناقصة ومحدودة من الاسفل 0 فانها متفاربة*
**نضع un+1=f(un),حيث f(x)=x2+x24.ومنه نجد
ℓ=f(ℓ) اذن ℓ=ℓ2+ℓ24. ℓ=0 و ℓ=2. ولدينا ℓ∈[0,1], اذنℓ=0.
المتتالية (un) والمعرفة كمايلي u0=−1 un+1=f(un)حيث f دالة معرفة على المجال [−2,+∞[ : f(x)=2√x+3.
- أدرس تغيرات الدالة f على [−2,+∞[.
- بين أن
- −1≤un≤un+1≤6
بين أن المتتالية متقاربة نحو العدد الحقيقي يطلب تعيينه.
- 1)
f′(x)=1√x+3. f′(x)>0 : f متزايدة على [−2,+∞[.
- **************2)
- لدينا
"−1≤un≤un+1≤6".التحقيف من أجل n=0 نجد
u0=−1 و u1=4 ادن −2≤u0≤u1≤6 اذن محققة
- نفرض ان
- n صحيحة من اجل كل عدد طبيعي −1≤un≤un+1≤6.
- نبرهن أن الخاصية من أجل n+1
- لدينا الدلة متزايدة على [−2,6][−2,6]
اذن الخاصية صحيحة من اجل كل عدد طبيعي
*********3)
بما ان المتتالية متزايدة من السؤال 2 ومحدودةمن الاعلى6 فانها متقاربة
- .النهاية ℓ∈[−1,6] . اذنf(ℓ)=ℓ, وعليه 2√ℓ+3=ℓ. بالتربيع نجد 4(ℓ+3)=ℓ2, ومنه ℓ=−2 و ℓ=6. ومن جهة اخرى ℓ∈[−1,6], وعليه ℓ=6 : المتتالية متقاربة نحو 6.
الرمز ∀ يعني من أجل كل عدد***
برهن أن
التحقيق

أي 2=2 محققة
نفرض صحة الخاصية من أجل كل عدد طبيعي n
أي 
نبرهن صحة الخاصية من أجل n+1
Un=3−2n⇔2Un=6−2n+1⇔2Un−3=3−2n+1⇔Un+1=3−2n+1
اذن Un+1=3−2n+1
التمرين السادس
برهن أن
**الحل**
التحقيق
 محققة
محققة
نفرض صحة الخاصية من أجل كل عدد طبيعي n 
نبرهن من اجل n+1 أي un+1 <2
**التمرين السابع**
نضع 
الحل
**التمرين الثامن** الحل
**التمرين التاسع**
الحل 
**التمرين العاشر**
الحل

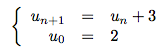
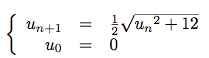
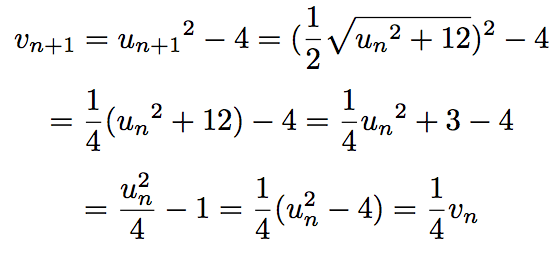

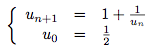
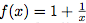 مع المستقيم ذو المعادلةة `y=x `
مع المستقيم ذو المعادلةة `y=x `