
متقن وادي أرهيو
اختبارات الفصل الاول
enseignement secondaire
السنة الثالثة ثانوي علمي
السنة الثالثة ثانوي أداب وفلسفة
السنة الثالثة ثانوي تسيير واقتصاد

.gif)

هام جدا
حل المعادلات التالية :
`ln(x)=1`
`ln(x)=-5`
نعتمد على القاعدة التالية `ln[米]=Delta` فان 米 = `e^Delta` ثم نستخرج المجهول المراد استخراجه من هذه المعادلة الاخيرة
S={e} مقبول `ln(x)=1 ⇔ x= e^1 =e` مع D : x > 0
S={ } مقبول `ln(x)=-5 ⇔ x= e^-5 = 1/e^5` مع D ; x > 0
`ln(x+4)=0 ⇔ x+4=e^0 ⇔ x=-4+1=-3 ` مجموعة تعرف المعادلة ]-4;+∞ [
x=-3 مقبول S={-3}
أحسب ` \lim_{x \rightarrow +\infty}\frac{x+1}{ln(x)}`
`\frac{x+1}{ln(x)}=\frac{x}{ln(x)}+\frac{1}{ln(x)}` ملاحضة [`a/infty=0 `]
` \lim_{x \rightarrow +\infty}\frac{x+1}{ln(x)} =`
` \lim_{x \rightarrow +\infty}\frac{x}{ln(x)}+\frac{1}{ln(x)}= `
` =+\infty+ 0 =+\infty `
حل المعادلة `ln(x)+ln(2)=3`
ايجاد مجموعة التعريف والتيسيط المعادلة باستخدهم الخواص `ln(ab)=ln(a)+ln(b) `
`D= ]0;+\infty[ `
`ln(x)+ln(2)= ln(2x)=ln(e^3) ` نعلم أن ( `ln(e^3)=3 `)
` 2x=e^3 `
` x=\frac{e^3}{2} `
`\frac{e^3}{2} \in ]0;+\infty[ `
` S={ \frac{e^3}{2} } `
حل المتراجحة `ln(x-1)+ln(2)\geq 4 `
ايجاد مجموعة التعريف والتيسيط المتراجحة باستخدهم الخواص `ln(ab)=ln(a)+ln(b) `
` x-1 > 0 `
` x-1 >0 \leftrightarrow x > 1 `
`D= ]1;+\infty[`
` ln(x-1)+ln(2)\geq 4 ; ln(2(x-1))\geq ln\left( e^4\right) `
` {ln(x-1)+ln(2)\geq 4} ; 2(x-1)\geq e^4 `
`{ln(x-1)+ln(2)\geq 4} leftrightarrow 2x\geq 2+ e^4 `
` {ln(x-1)+ln(2)\geq 4} leftrightarrow x\geq 1+ \frac{e^4}{2} `
` S=\left[1+ \frac{e^4}{2};+\infty [ `
عند ايجاد الحل نتقوم بتقاطع المجال المحصل عليه مع مجموعة التعريف نتحصل على الحل النهائي
` `
` e^{2x}+e^x-6=0 `
بوضع`X=e^x و X^2=\left(e^x\right)^2=e^{2x}` نحل معادلة من الدرجة 2 باستخدام المميز
بوضع `X=e^x و X^2=e^{2x} ` نجد
` X^2+X-6=0 `
` \Delta=b^2-4ac=1^2-4\times 1 \times (-6)=25 `
` X_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-1 + 5 }{2 }=2 `
` X_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-1 - 5 }{2 }=-3 `
لدينا ` e^x=X_1=2\leftrightarrow x=ln(2) `
وكذلك` e^x=X_2=-3 ` مرفوض لان` e^x ` موجب تماما
`S={ ln(2)}`
حل المعادلة التالية
` -2ln^2(x)+7ln(x)-6=0 `
بوضع `X=ln(x) ` وتعين مجموعة التعريف
` D= ]0;+\infty[`
بوضع ` X=ln(x) ` نجد
` -2X^2+7X-6=0 `
`\Delta=b^2-4ac=7^2-4\times (-2)\times (-6)=49-48=1 `
`X_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{ -7+ 1 }{-4 }=\frac{-6}{-4}=\frac{2}{3}`
`X_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{ -7- 1 }{-4 }=\frac{-8}{-4}=+2`
لدينا ` ln(x)=X_1=\frac{2}{3}\leftrightarrow x=e^{\frac{2}{3}} `
و` ln(x)=X_2=+2\leftrightarrow x=e^{2} `
الحلان مقبولان ينتميان الى مجموعة التعريف
` S={ e^{2}; e^{\frac{2}{3}} }`
`\e^x=5 ; 5\e^x=10 ; \e^x=-1 ; \e^{2x+3}=1 `
*****************************************************************************
` \e^x=5 \ ي أ \e^x=\e^{\ln 5} \ ي أ x=\ln 5 `
` 5\e^x=10 \ي أ \e^x=2 \ي أ \e^x=\e^{\ln 2}\ي أ x=\ln 2 `
ليس لها حل لان دالة exp موجبة تماما
` \e^{2x+3}=1\ ي أ \e^{2x+3}=\e^0 \ \ ي أ 2x+3=0\ \ ي أ 2x=-3\ \ ي أ x=-\frac{3}{2}`
حل المعادلات الاتية
` 1) \ln x=3 ; 2) \ln(2x-3)=1 3) \ln(1-x)=\ln(x+3) 4) \ln(2x-3)=1 `
**********************************************************************************************************************1) `D=]0;+\infty[ `
مقبول ينتمي الى مجموعة التعريف`\ln x=3 \ ي أ \ln x=\ln \left(\e^3\right) \ ي أ x=\e^3 `
2) ` D=]\frac{3}{2};+\infty\[ `
` \ln(2x-3)=1\ ي أ \ln(2x-3)=\ln \e \ \ ي أ 2x-3=\e \ \ ي أ 2x=3+\e\ \ ي أ x=\frac{3+\e}{2} `
مقبول ينتمي الى مجموعة التعريف
3)`D= ]-3;1[`
` \ln(1-x)=\ln(x+3) \ي أ 1-x=x+3 \ \ي أ -2=2x \ \ي أ x=-1 `
حل مقبول `-1\in ]-3;1[ `
أدرس أشارة الدالة `f`على المجال`]0;+\infty[ ` في كل حالة من الحالات الاتية
1) `f(x)=2\ln x+4`
2) `f(x)=5\ln x-20`
3) `f(x)=-5-3\ln x`
4) `f(x)=(x-2)\ln x`
1) `D= ]0;+\infty[ `
`2\ln x+4>0\ي أ 2\ln x>-4\ي أ \ln x>-2\ي أ x>\e^{-2} `
جدول الاشارة
2) `D= ]0;+\infty[ `
`5\ln x-20>0 \ي أ 5\ln x>20 \ي أ \ln x >4 \ي أ x>\e^4 `
جدول الاشارة
3) `D= ]0;+\infty[ `
` -5-3\ln x>0\ي أ -3\ln x>5\ي أ \ln x<- e="" frac="" nbsp="" p="" x="">
جدول الاشارة
4) `D= ]0;+\infty[ `
جدول الاشارة
عين مجموعة التعريف الدالة
f(x) = ln(x) + ln(2 - x)
(x > 0 وx < 2) ⇔ 0 < x < 2.
`D_f=]0;2[`
عين مجموعة التعريف الدالتين
التمرين الاول
` f(x)=\frac{\ln x}{x} و D= ]0 ;+\infty[ `
أحسب `f^'(x)`
مشتق قسمة دالتين` f'(x)=\frac{u'v-uv'}{v^2} `
`f'(x)=\frac{\frac{1}{x}\times x - \ln x \times 1}{x^2} `
`f'(x)=\frac{1-\ln x}{x^2} `
`f :x \mapsto 3-x+2\ln x و D= ]0 ;+\infty[ `
أحسب `f^'(x)`
`f'(x)=-1+\frac{2}{x}=\frac{2-x}{x} `
أحسب المشتقة
أدرس اشارة الدالة `f` على `R`
1) `f(x)=\e^x-1`
2) `f(x)=2\e^{-3x}-8`
*******************************************************************************************************************1) `\e^x-1>0 \ي أ \e^x >1 \ي أ x>0 `
جدول الاشارة
2) ` 2\e^{-3x}-8>0 \ي أ 2\e^{-3x}>8 \ \ي أ \e^{-3x}>4 \ \ي أ -3x>\ln 4 \ \ي أ x<- 4="" frac="" ln="" p="">
جدول الاشارة
لتكن الدالة `f` والعرفة كمايلي
` f(x)=3x\ln x-9x+10`
1) عين مجموعة التعريف الدالة
3)أحسب المشتقة
4)أحسب النهايات
5) شكل جدول التغيرات
********************************************************************************************************************* التمرين الاول*الجزء الاول*
لتكن الدالة `f` والعرفة كمايلي
`f(x) = 2\e^x + 2x – 7`
1) عين مجموعة التعريف الدالة
2)أحسب المشتقة
3)أحسب النهايات
4) شكل جدول التغيرات
5)بين أن المعادلة `f(x)=0` تقبل حل وحيد `alpha` حيث `alpha \in ]0.940;0.941[`
6) استنتج اشارة الدالة `f`
1)`D_f=R`
2) ` f'(x) = 2\e^x + 2 = 2(e^x + 1) ` المشتقة موجبة تماما لان `e^x `موجب
3) `\lim\_{x \to +\infty} f(x) = +\infty ` و `\lim\_{x \to +\infty} f(x) = -\infty ` لان ` \lim\_{x \to -\infty} \e^x=0 `
جدول التغيرات
5) مبرهنة القيم المتوسطة :الدالة`f`معرفة ومستمرة ورتيبة على المجال ]0.940;0.941[(متزايدة) `f(0,940) \approx-3,7 \times 10^{-5} < 0 و f(0,941) \approx 0,007 > 0`حسب م ق م المعادلة تقبل حل وحيد ` alpha` على هذا المجال
6) اشارة الدالة`f`
*الجزء الثاني*
نضع `g(x) = (2x – 5)(1 – \e^{-x}) `
1)شكل جدول تغيرات الدالة ` g`
2)بين أن ` g(\alpha) = \frac{(2\alpha – 5)^2}{2\alpha – 7}`
نضع `h : x \mapsto \frac{(2x – 5)^2}{2x – 7}`
3) أدرس اتجاه تغير الدالة `h`
4)استنتج حصر للعبارة ` g(alpha)`
************************************************************************************************************************************************************النهايات `\lim\_{x \to -\infty} g(x) = +\infty و \lim\_{x \to +\infty} g(x) = +\infty `
المشتقة ` g'(x) = 2\left(1 – \e^{-x}\right) + \e^{-x}(2x – 5) \ = 2 – 2\e^{-x} + 2x\e^{-x} – 5\e^{-x} \ = 2 – 7\e^{-x} + 2x \e^{-x} \ = \left(2\e^{x} – 7 + 2x\right)\e^{-x} \ = f(x)\e^{-x} `
ومنه`g^'(x)=f(x)\e^{-x}`
جدول تغيرات الدالة `g`
ملاحضة في جدول التغيرات بدل `f` نضع `g` والعكس خطأفي الكتابة
2) `f(\alpha) = 2\e^{\alpha} + 2\alpha – 7 =0 ` ومنه ` \e^{-\alpha} = \frac{2}{7 – 2\alpha} `
ولدينا
` g(\alpha) = (2\alpha – 5) \times \left(1 – \frac{2}{7 – 2\alpha}\right) \ = (2\alpha – 5) \times \frac{7 – 2\alpha – 2}{7 – 2\alpha} \ = (2\alpha – 5) \times \frac{5 – 2\alpha}{7 – 2\alpha} \ = (2\alpha – 5) \times \frac{2\alpha – 5}{2\alpha – 7} \ = \frac{(2\alpha – 5)^2}{2\alpha – 7} `
ومنه`g(\alpha)=\frac{(2\alpha – 5)^2}{2\alpha – 7} `
3) ` h'(x) = \frac{2\times 2(2x – 5)(2x – 7) – 2(2x – 5)^2}{(2x – 7)^2} \ = \frac{2(2x – 5)\left(2(2x – 7) – (2x – 7)\right)}{(2x – 7)^2} \ = \frac{2(2x – 5)(4x – 14 – 2x + 5)}{(2x – 7)^2} \ = \frac{2(2x – 5)(2x – 9)}{(2x – 7)^2} `
جدول الاشارة للمشتقة
ومنه الدالة `h` متناقصة على المجالين *****; ومتزايدة على المجالين ****
4) الدالة ` h ` متزايدة على المجال `]-\infty;\frac{5}{2}\] `
ومنه` h(0,940) < h(\alpha) < h(0,941) `
وعليه ` -1,901 < g(\alpha) < -1,900 `
1) شكل جدول تغيرات الدالة
2) اشتنتج اشارة الدالة
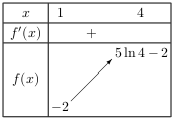
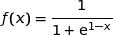 و D=R
و D=R
1) أدرس اتجاه تغير الدالة 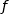 على مجموعة التعريف
على مجموعة التعريف
2)بين أن 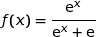
1) 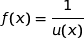
حيث 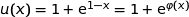
اذن 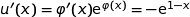
وأخيرا 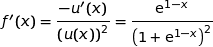
لدينا
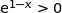 ✔
✔
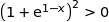 ✔
✔
وبالتالي 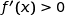 .
.
ومنه 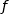 متزايدة تماما على R
متزايدة تماما على R
2)
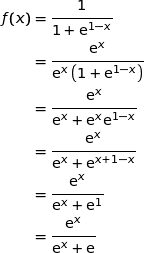
اذن 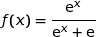
على المجال 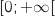 نضع
نضع 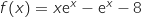 .
.
1) أحسب النهايات على أطراف مجموعة التعريف
2) أحسب المشتقة
3) شكل جدوت التغيرات الدالة
4) بين أن المعادلة f(x)=0 تقبل حل وحيد  . على
. على 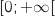
5) تحقق أن 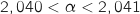 .
.
1)
لدينا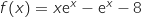 .ومنه
.ومنه 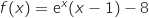 ,
,  عند
عند  .
.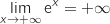 و
و 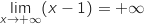 الجداء
الجداء 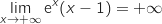 .نحصل على
.نحصل على 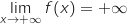 .
.2)
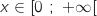 ,
, 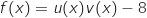 مع
مع 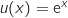
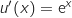
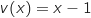
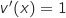 اذن
اذن 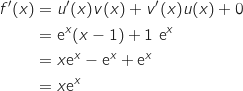
3)
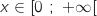 ,
, 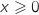 و
و 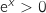 , ومنه
, ومنه 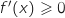 جدول تغيرات الدالة f
جدول تغيرات الدالة f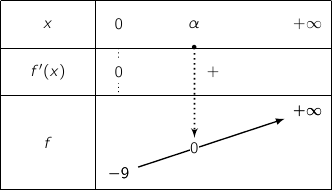
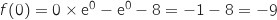
4)الدالة معرفة ومستمرة ورتيبة (متزايدة) على ![]() ولدينا :
ولدينا :
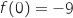
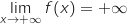
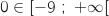 , حسب م ق م المعادلة
, حسب م ق م المعادلة 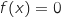 حل وحيد
حل وحيد 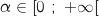 .
.5)بالحاسبة نجد
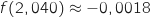
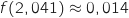
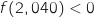 et
et 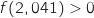 , اذن
, اذن 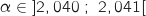 .
.6)

لتكن الدالة  والمعرفة على المجال
والمعرفة على المجال  كمايلي:
كمايلي:
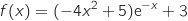
1) بين أن
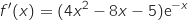
2) ادرس اشارة 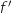 على
على  .
.
3) بين أن من اجل 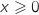 , فان
, فان 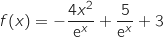 .
.
4) احسب نهاية  عند
عند  .
.
4) فسر النتية هندسيا
5) شكل جدول تغيرات  .
.
4. بين ان المعادلة 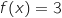 تقبل حل وحيد
تقبل حل وحيد 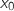 على المجال
على المجال  .
.
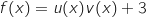 ,حيث
,حيث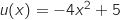 و
و 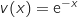 ,ومنه
,ومنه 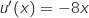 و
و 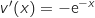 .مشتق جداء دلتين:
.مشتق جداء دلتين: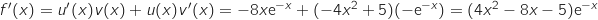
2)
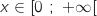 ,
, 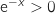 , اشارة
, اشارة  من اشارة
من اشارة 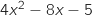 .
. 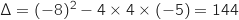 .:
.: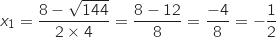
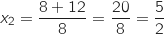 .
.
3) 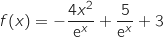 .
.
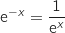 وبالتالي
وبالتالي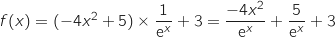 .
.4)
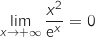 , ومنه
, ومنه 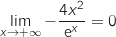 .
.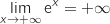 أي
أي 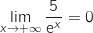 .اذن
.اذن 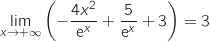 .
.5)
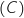 مستقيم مقارب
مستقيم مقارب 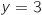 عند
عند  .
.6) جدول التغيرات
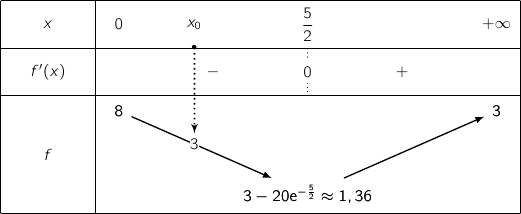
7)
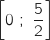 ,
,  مستمرة ورتيبة , و
مستمرة ورتيبة , و 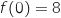 و
و 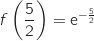 .بما ان
.بما ان 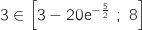 , حسب م ق م
, حسب م ق م 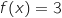 تقبل حل وحيد
تقبل حل وحيد 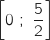 .
.  معرفة على المجال
معرفة على المجال 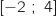 .
.
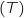 المماس للمنحنى
المماس للمنحنى 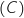 في B ذو المعادلة
في B ذو المعادلة 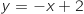 .
.
1) عين 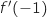 .
.
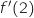 .
.3) فسر هندسيا 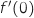 , ثم عين قيمته
, ثم عين قيمته
1) نضع 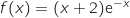 .
.
2) عين احداثيات A من المنحنى 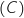 .
.
3) باستخدام الدالة  شكل جدول تغيرات الدال على
شكل جدول تغيرات الدال على 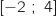 .
.
1) 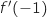 .
.
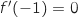 .
.2) 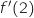 .
.
 متناقصة تماما على
متناقصة تماما على 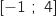 , وعليه من أجل كل
, وعليه من أجل كل 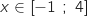 ,
,  سلبة أي
سلبة أي 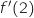 سالب
سالب التفسير 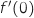
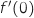 معامل توجيه المماس للمنحنى في النقطة ذات الفاصلة 0.و معادلة المماس هي
معامل توجيه المماس للمنحنى في النقطة ذات الفاصلة 0.و معادلة المماس هي 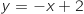 , ومنه
, ومنه 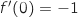
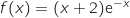 .
.
1)
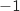 ,ومنه
,ومنه 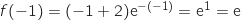 . A(-1.e)
. A(-1.e)3) جدول التغيرات على 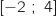 .
.
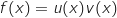 مع
مع 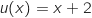 ;
; 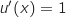 و
و 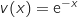 ;
; 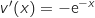 اذن
اذن 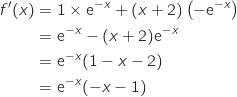 من اجل كل
من اجل كل  ,
, 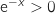 ,اشارة
,اشارة  من اشارة
من اشارة 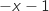 و منه الجدول
و منه الجدول 
الدالة F معرفة على  كمايلي
كمايلي 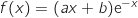
1) بين أن 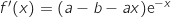 .
.
2) علما أن 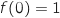 و
و 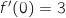 . استنتج
. استنتج  و
و  .
.
1) 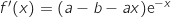 .
.
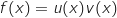 مع
مع 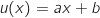
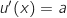
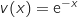
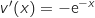 وعليه
وعليه 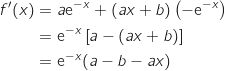
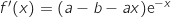 .
.2) لدينا 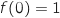 و
و 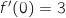 .
.
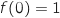 ,ومنه
,ومنه 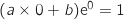 , اذن
, اذن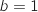 .
.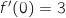 , ومنه
, ومنه 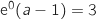 وعليه
وعليه 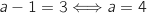 .
.الدالة  معرفة على
معرفة على 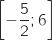 .
.
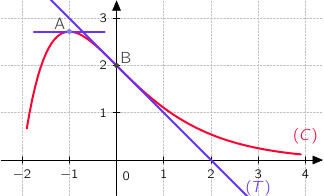
و 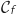 تمثيلها البياني
تمثيلها البياني
A 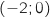 , و B
, و B 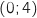 , و C
, و C 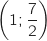 , D
, D 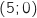 E (6.0).
E (6.0).
(CE) المماس للمنحنى 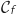 في C
في C
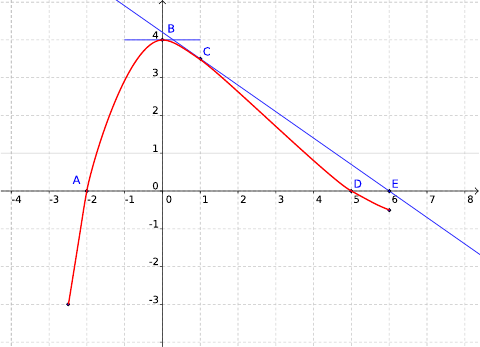
 و
و 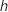 دالتان معرفتان كمايلي
دالتان معرفتان كمايلي 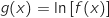 و
و 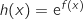 .
.
1)  معرفة على
معرفة على
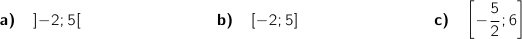
2) ..............= 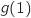
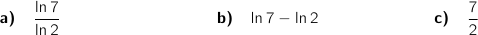
3) ............ =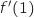
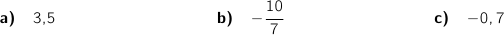
4) ..................... = 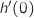
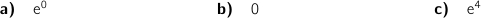
1)
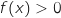 .ومنه
.ومنه 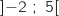 .يعني a).
.يعني a).2)
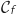 يمر بالنقطة
يمر بالنقطة 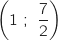 ومنه
ومنه 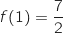
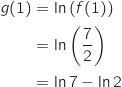
3):
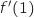 معامل توجيه المماس
معامل توجيه المماس 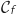 في C. وهو المستقيم (CE).ومنه :
في C. وهو المستقيم (CE).ومنه : 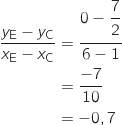 الاجابة c).
الاجابة c).4)
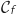 أفقي ومنه
أفقي ومنه 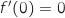 ولدينا
ولدينا 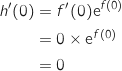 الاجابة b).
الاجابة b).
الجزء 1
 معرفة على
معرفة على 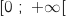 كمايلي
كمايلي 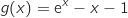
 .
.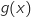
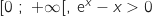 بين انه من اجل كل Xمن .
بين انه من اجل كل Xمن . دالة معرفة على
دالة معرفة على  كمايلي
كمايلي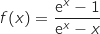
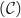 تمثيلها البياني في الاسفل
تمثيلها البياني في الاسفل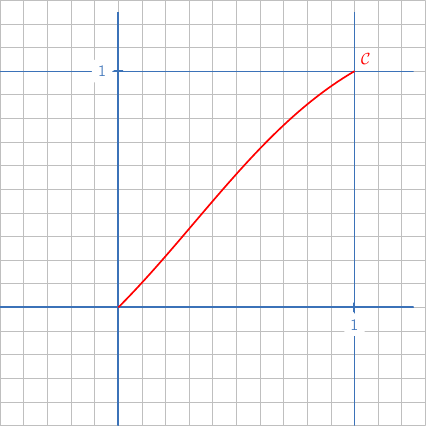
 من [0 ; 1], فان
من [0 ; 1], فان 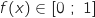 .2) (D)
.2) (D) 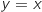 .a. بين أنه من أجل كل
.a. بين أنه من أجل كل  من [0 ; 1],
من [0 ; 1], 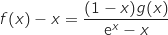 .b. أدرس الوضعية بين (D) و
.b. أدرس الوضعية بين (D) و 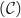 على
على  .
.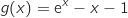
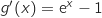 ,
, 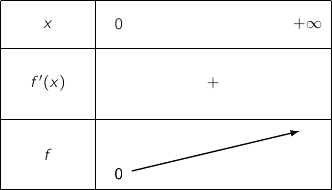
2)
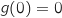 و
و 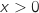 والدالة متزايدة ومنه,
والدالة متزايدة ومنه, 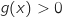 .
.3)  من
من 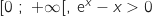 .
.
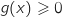 من أجل
من أجل 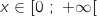 , يعني
, يعني 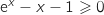 أي
أي 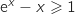 وبالتالي
وبالتالي 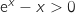 .
.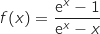
 متزايدة تماما على [0 ; 1].
متزايدة تماما على [0 ; 1].
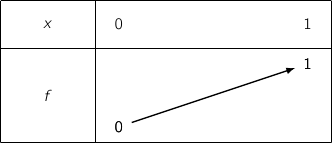
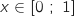 ,فان
,فان 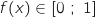 .
.2) .
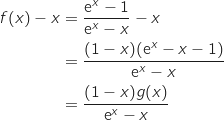
3). )
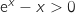 , على
, على  , ومنه اشارة
, ومنه اشارة 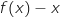 من اشارة
من اشارة 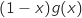 .على المجال المعطى في التمرين
.على المجال المعطى في التمرين 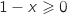 و
و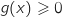 , وعليه
, وعليه 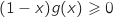 , اذن
, اذن 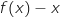 موجب
موجب 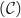 فوق
فوق 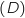 . نلاحض أن
. نلاحض أن 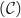 و
و 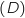 يتقاطعان عند
يتقاطعان عند 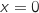 و
و  .
.f و g معرفتان على  كمايلي
كمايلي
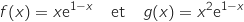
f و g تمثيلهما  et
et 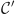 على الترتيب
على الترتيب
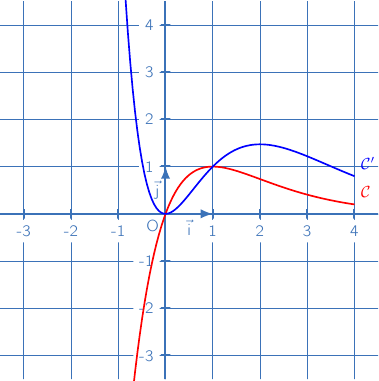
1) أحسب نهاية الدالة f و g عند  .
.
2) 1) أحسب نهاية الدالة f و g عند  .
.
1)
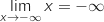
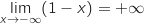 ومنه :
ومنه : 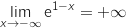
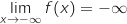 .
.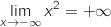
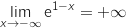
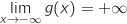 .
.
2)
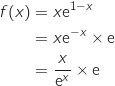
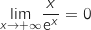 .ومنه
.ومنه 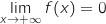 .
.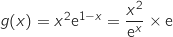 , لدينا
, لدينا 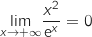 ومنه
ومنه 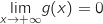 .
.3)
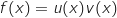 مع
مع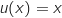 , ومنه
, ومنه 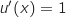
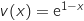 ,ومنه
,ومنه 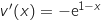
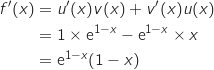 من اجل
من اجل  ,
, 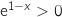 , اشارة
, اشارة  من اشارة
من اشارة 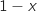 .
.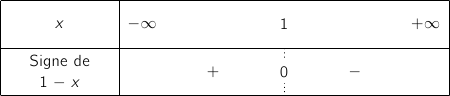
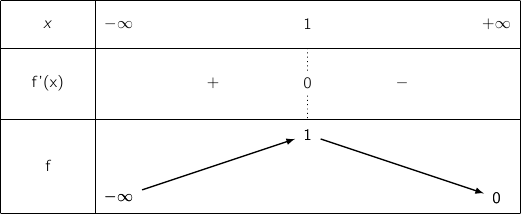
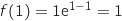
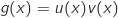 حيث
حيث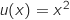 , ومنه
, ومنه 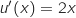
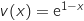 , زمنه
, زمنه 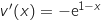
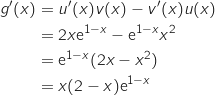 اشارة
اشارة 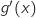 من اشارة
من اشارة 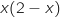 .:
.:
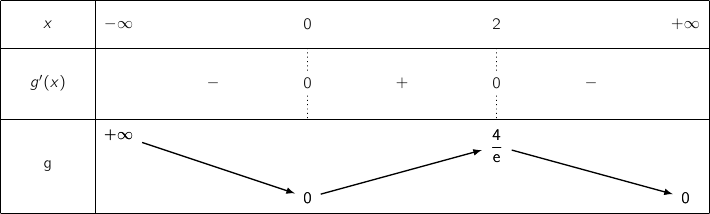
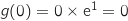
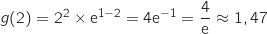
 معرفة على المجال
معرفة على المجال 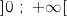 كمايلي
كمايلي
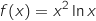
1) أحسب نهاية  عند
عند  .
.
2) شكل جدول تغيرات  على
على 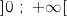 .
.
3) بين أنه يوجد مماس وحيد للمنحنى  يمر بالنقطة O. يطلب كتابة المعادلة
يمر بالنقطة O. يطلب كتابة المعادلة
1)
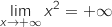 و
و 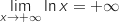 , ومنه
, ومنه 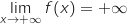 .
.2)
مشتق جداء دالتين
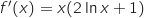 .اشارة
.اشارة  من اشارة
من اشارة 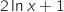 . لان x موجبومنه
. لان x موجبومنه 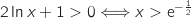 .
. 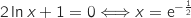 و
و 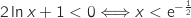 جدول التغيرلت
جدول التغيرلت 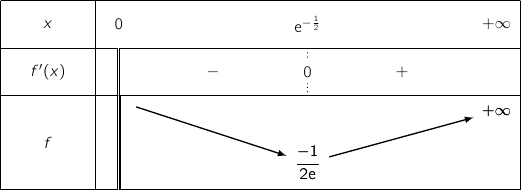
3)
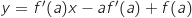 .المماس يمر بالنفطة 0 معناه
.المماس يمر بالنفطة 0 معناه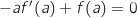 .بالتلي:
.بالتلي: 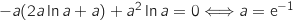 . وعليه يوجد حل وحيد
. وعليه يوجد حل وحيد 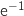 .
. 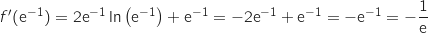 .معادلة المماس هي
.معادلة المماس هي 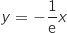 .
. و D=
و D=  حيث
حيث
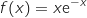
1) ............................... = 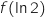

2) المشتقة هي .....................................


3) معادلة المماس عند 0 هي .......................... :

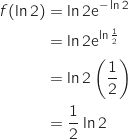 الاجابة d.
الاجابة d.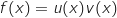 مع
مع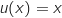 ;
; 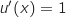
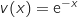 ;
; 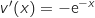 ومنه
ومنه 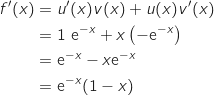 الاجابة c.
الاجابة c.
3)
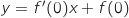 حيث
حيث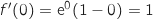 et
et 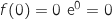 ومنه
ومنه 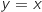 .الاجابة c.
.الاجابة c. 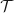 المماس عند
المماس عند 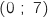 .
.
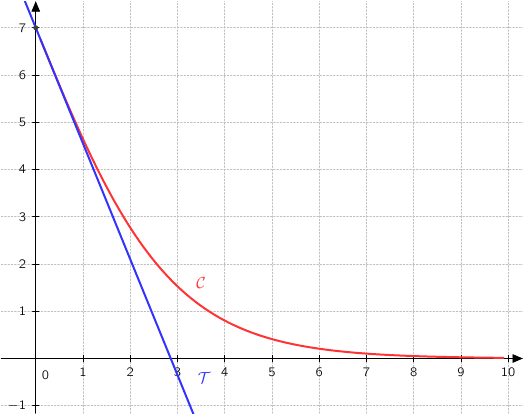
1) عين 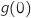 .
.
2) 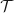 المماس يمر بالنقطة
المماس يمر بالنقطة 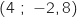 .
.
أحسب 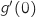
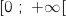 كمايلي
كمايلي 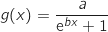
a) بين أن 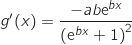 .
.
b) استنتج قيمة  و
و  .
.
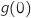 .
.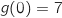 .
.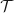 المماس يمر بالنقطتين
المماس يمر بالنقطتين 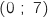 و
و 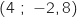
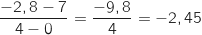
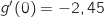
3)
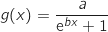
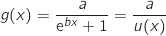 حيث
حيث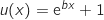
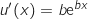 ومنه
ومنه 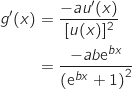
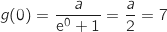
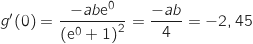
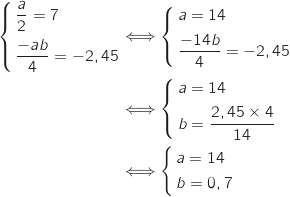
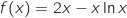 و D=]0; +∞ [
و D=]0; +∞ [ 1). ....................=
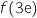 a)
a) 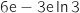 b)
b) 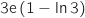 c)
c) 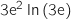 2). حلول المعادلة
2). حلول المعادلة 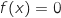 هي :a)
هي :a) 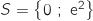 b)
b) 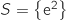 c)
c) 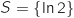
1)
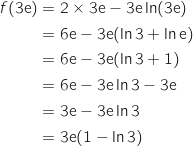
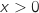 :
: 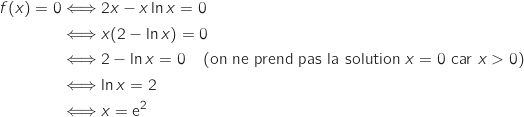
النهايات
التمرين الاول
f(x)=ex+ex-−4x−2. و ]+∞ ; 0]= D
1) تحقق أن
f(x)=x(xex一−4)+ex-−2.
2) أحسب نهاية الدالة على مجموعة التعريف
1) ننشر نتحصل على العبارة f(x)
2) عند +∞ نتحصل على +∞
قواعد مهمة
x > 0 y∈ R
, lnx=y, ⇔ ey=x
elnx=x
lnex=x x من R,
ln1=0
lne=1
{x∈]0,+∞[y=lnx⟺x=ey
xو y من ]0,+∞[,
lnxy=lnx+lny
ln1x=−lnx
lnxy=lnx−lny
ln√x=12lnx
lnxn=nlnx
a1,a2,...,an موجبة تماما
ln(a1a2...an)=lna1+lna2+...lnan
limx→+∞lnx=+∞
limx→0lnx=−∞
limx→+∞lnxxr=0 مع r>0
limh(x)→0ln(1+h(x))h(x)=1
limx→0xrlnx=0 مع r>0
(lnx)′=1x
x>0,y>0,
x<y⟺lnx<lny
x=y⟺lnx=lny
(ln(u))′=u′(x)u(x)
***********************************************************************************************************************
أحسب مشتقة الدالة `f` في كل حالة من الحلات الاتية
1)`f(x) = [ln(x)]^3`
2) `f(x) = ln(2x^2 - 4)`
3) `f(x) = [ln(ln(x))]^2`
1)` f^'(x)=3 \cdot \left( \frac{1}{x}\right)\cdot[ln(x)]^2`
2)` f'(x) = \frac{1}{2x^2 - 4} \cdot 4x \ = \frac{4x}{2x^2 - 4} `
3)` f'(x) = 2[ln(ln(x))] \cdot \ \frac{1}{ln(x)}\cdot \frac{1}{x} \ = \frac{2 ln(ln(x))}{x\cdot ln(x)}`
التمرين
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول
وضع التمرين الاول
حل التمرين الاول