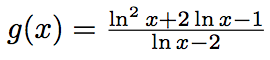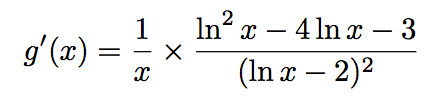GUEBLI MATHS

هام جدا "جميع المعلومات السنة الماضية تجدها هنا ما عليك ايجاد الحل ثم مشاهدة الحل بعد المحاولة الاستاذ قبلي"

عناصر المراجعة

1)   المشتقات

2) معادلة المماس 

3) نقطة الانعطاف

4)  شفعية  دالة

5) اشارة كثير حدود من الدرجة 2 مع أمثلة

6)  النهايات والمستقيمات المقاربة

7) دراسة تغيرات دالة 

8) كل ما يتعلق بالدالتين ln و exp

الموضوع الاول

التمرين الاول 

المشتقات

لتكن الدالة العددية  `ƒ`  ذات المتغير الحفيفي`x` كمايلي

     D=ℝ          ` f(x)=3x^3-5x^2+3x-2 ` 

 D=ℝ                   ` f(x)= (3x-1)/(x^2 +3 `

 D=ℝ        ` f(x)= (3x-1)^2/(x^2 +3)^2 `

D=ℝ               ` f(x)= (3x-1)^2(x^2 +3) `

  ]+∞;0]` = d         ` f(x)= sqrt(2x^3+x^2-3x+1) `                                      

 ` `f(x)= (2x-6)sqrt(-3x+1)                   d=]-∞;0]`

       ]-∞;0]` = d             ` f(x)= (2x-6)/sqrt(-3x+1) `        

D=ℝ                  ` f(x)= cos(2x-6) `

D=ℝ               ` f(x)= 3sin(2x^2-6) `

أحسب في كل حالة من الحالات السابقة      `f^'(x) `

`

حل التمرين الاول

ملاحضة1 مشتق العبارة    

  `(a x^n )^'=n.a x^(n-1)`  

و `(ax)^'=a`   و   `(a)^'=0`

جميع هذه الدوال قابلة للاشتقاق على مجموعة تعريفها

1)   ``f^'(x)=9x^2-10x+3`

2)   `f^'(x)=((3)(x^2+3)-(2x)(3x-1))/(x^2+3)^2`                  ثم النشر والتبسيط  لا ينصح نشر المقام    

ملاحضة2 مشتق العبارة

`(..........)^n'=n(...........)^'(.........)^(n-1)`

مثال

`(x^2+3)^2'=2(2x)(x^2+3)^(2-1)=4x(x^2+3)`

3)`f^'(x)=(2(3)(3x-1)(x^2+3)^2-2(2x)(x^2+3)(3x-1)^2)/(x^2+3)^4`

4)` f^'(x)=2(3)(3x-1)(x^2+3)+(3x-1)^2 2x`

ملاحضة3 مشتق العبارة

`sqrt((..........))^'=(.................)^'/(2sqrt((.............))`

5) `f^'(x)=(6x^2+2x-3)/(2sqrt(2x^3+x^2-3x+1)`

اغلاق المشاهدة

*********************************

التركيز على مشتق القسمة والجداء

مثال

``[f(x)=frac{x^3-2x^2-5x-1}{2x+3}]``

مشتف حاصل قسمة دالتبن  `f=frac{u}{v} `

تذكير

 ` [f'=frac{u'v-v'u}{v^2}]` 

حيث `[u(x)=x^3-2x^2-5x-1] و [v(x)=2x+3]`

 `[u'(x)=3x^2-4x-5] و [v'(x)=2]` 

 `f'(x)=((3x^2-4x-5)(2x+3)-2(x^3-2x^2-5x-1))/(2x+3)^2 =frac{4x^3+5x^2-12x-13}{(2x+3)^2}`

 

**تماربن متنوعة**

حساب المشتقة باستخدام التعريف

التمرين الاول

$$f\left(x\right)=2x^3-1$$

أحسب مشتقة الدالة f باستخدام التعريف

 

$$f^{\prime }\left(x\right)=\underset{h\to 0}{lim}\frac{f\left(x+h\right)-f\left(x\right)}{h}=\underset{h\to 0}{lim}\frac{2{\left(x+h\right)}^3-1-\left(2x^3-1\right)}{h}$$

$$\begin{array}{cc}{f}^{\prime }\left(x\right)& =\underset{h\to 0}{lim}\frac{2\left(x^3+3x^{2}h+3x{h}^2+h^3\right)-1-2x^3+1}{h}\\ & =\underset{h\to 0}{lim}\frac{2x^3+6x^{2}h+6x{h}^2+2h^3-1-2x^3+1}{h}\\ & =\underset{h\to 0}{lim}\frac{h\left(6x^2+6xh+2h^2\right)}{h}=\underset{h\to 0}{lim}\left(6x^2+6xh+2h^2\right)=6x^2\end{array}$$

$$f^{\prime }\left(x\right)=6x^2$$

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الثاني

نفس السؤال السابق

$$V\left(t\right)=\frac{t+1}{t+4}$$

$$V^{\prime }\left(t\right)=\underset{h\to 0}{lim}\frac{V\left(t+h\right)-V\left(t\right)}{h}=\underset{h\to 0}{lim}\frac{1}{h}\left(\frac{t+h+1}{t+h+4}-\frac{t+1}{t+4}\right)$$

$$V^{\prime }\left(t\right)=\underset{h\to 0}{lim}\frac{1}{h}\left(\frac{\left(t+h+1\right)\left(t+4\right)-\left(t+1\right)\left(t+h+4\right)}{\left(t+h+4\right)\left(t+4\right)}\right)$$

.

$$\begin{array}{cc}{V}^{\prime }\left(t\right)& =\underset{h\to 0}{lim}\frac{1}{h}\left(\frac{t^2+th+5t+4h+4-\left(t^2+th+5t+h+4\right)}{\left(t+h+4\right)\left(t+4\right)}\right)\\ & =\underset{h\to 0}{lim}\frac{1}{h}\left(\frac{t^2+th+5t+4h+4-t^2-th-5t-h-4}{\left(t+h+4\right)\left(t+4\right)}\right)\\ & =\underset{h\to 0}{lim}\frac{1}{h}\left(\frac{3h}{\left(t+h+4\right)\left(t+4\right)}\right)=\underset{h\to 0}{lim}\frac{3}{\left(t+h+4\right)\left(t+4\right)}=\frac{3}{{\left(t+4\right)}^2}\end{array}$$

$$V^{\prime }\left(t\right)=\frac{3}{{\left(t+4\right)}^2}$$

مشاهدة حل التمرين الثاني اغلاق المشاهدة

التمرين الثالث

نفس السؤال السابق

$$f\left(x\right)=\sqrt{1-9x}$$

 

.

$$f^{\prime }\left(x\right)=\underset{h\to 0}{lim}\frac{f\left(x+h\right)-f\left(x\right)}{h}=\underset{h\to 0}{lim}\frac{\sqrt{1-9\left(x+h\right)}-\sqrt{1-9x}}{h}$$

$$f^{\prime }\left(x\right)=\underset{h\to 0}{lim}\frac{\left(\sqrt{1-9\left(x+h\right)}-\sqrt{1-9x}\right)}{h}\frac{\left(\sqrt{1-9\left(x+h\right)}+\sqrt{1-9x}\right)}{\left(\sqrt{1-9\left(x+h\right)}+\sqrt{1-9x}\right)}$$

$$\begin{array}{cc}{f}^{\prime }\left(x\right)& =\underset{h\to 0}{lim}\frac{1-9\left(x+h\right)-\left(1-9x\right)}{h\left(\sqrt{1-9\left(x+h\right)}+\sqrt{1-9x}\right)}=\underset{h\to 0}{lim}\frac{1-9x-9h-1+9x}{h\left(\sqrt{1-9\left(x+h\right)}+\sqrt{1-9x}\right)}\\ & =\underset{h\to 0}{lim}\frac{-9h}{h\left(\sqrt{1-9\left(x+h\right)}+\sqrt{1-9x}\right)}=\underset{h\to 0}{lim}\frac{-9}{\sqrt{1-9\left(x+h\right)}+\sqrt{1-9x}}=\frac{-9}{2\sqrt{1-9x}}\end{array}$$

$$f^{\prime }\left(x\right)=\frac{-9}{2\sqrt{1-9x}}$$

مشاهدة حل التمرين الثالث اغلاق المشاهدة

التمرين الرابع

أحسب المشتقة باستخدام الخواص

 $h\left(z\right)=\left(1+2z+3z^2\right)\left(5z+8z^2-z^3\right)$ .

مشتق جداء دالتين 

$$\begin{array}{cc}{h}^{\prime }\left(z\right)& =\left(2+6z\right)\left(5z+8z^2-z^3\right)+\left(1+2z+3z^2\right)\left(5+16z-3z^2\right)\\ & =5+36z+90z^2+88z^3-15z^4\end{array}$$

مشاهدة حل التمرين الخامس اغلاق المشاهدة

التمرين السادس

أحسب المشتقة باستخدام الخواص

 $g\left(x\right)=\frac{6x^2}{2-x}$ .

مشتق حاصل قسمة دالتين

$$g^{\prime }\left(x\right)=\frac{12x\left(2-x\right)-6x^2\left(-1\right)}{{\left(2-x\right)}^2}=\frac{24x-6x^2}{{\left(2-x\right)}^2}$$

مشاهدة حل التمرين السادس اغلاق المشاهدة

التمرين 7

أحسب المشتقة باستخدام الخواص

 $R\left(w\right)=\frac{3w+w^4}{2w^2+1}$ .

مشتق حاصل قسمة دالتين

$$R^{\prime }\left(w\right)=\frac{\left(3+4w^3\right)\left(2w^2+1\right)-\left(3w+w^4\right)\left(4w\right)}{{\left(2w^2+1\right)}^2}=\frac{4w^5+4w^3-6w^2+3}{{\left(2w^2+1\right)}^2}$$

مشاهدة حل التمرين 7 اغلاق المشاهدة

التمرين8

أحسب المشتقة باستخدام الخواص

$f\left(x\right)=\frac{x-x^2}{1+8x^2}$

 

مشتق حاصل قسمة دالتين

$$f^{\prime }\left(x\right)=\frac{\left(1-2x\right)\left(1+8x^2\right)-\left(x-x^2\right)\left(16x\right)}{{\left(1+8x^2\right)}^2}=\frac{1-2x-8x^2}{{\left(1+8x^2\right)}^2}$$

مشاهدة حل التمرين 8 اغلاق المشاهدة

**الدالة الاسية  EXP**

 مشتق دالة  exp

`[e^f(x)]^'=f^'(x).e^f(x)`

*التمرين الاول*

` f(x)=1+\left(-4x^2-10x+8\right)\e^{-0,5x} و D=R `

أحسب  `  f^'(x)`    (مشتق جداء دالتين)

  `   f'(x)=\left(-4\times 2x-10\right)\e^{-0,5x}+\left(-4x^2-10x+8\right)\times (-0,5)\e^{-0,5x} \ =`

`\left(-8x-10+2x^2+5x-4\right)\e^{-0,5x} \ =`

`\left(2x^2-3x-14\right)\e^{-0,5x} `

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين 2

` f(x)=-\frac{\e^x}{\e^x+1}  و D=R` 

 أحسب `f^'(x)`     

` f'(x)=-\frac{\e^x\left(\e^x+1\right)-\e^x\times \e^x}{\left(\e^x+1\right)^2} \ =-\frac{\e^{2x}+\e^x-\e^{2x}}{\left(\e^x+1\right)^2} \ =-\frac{\e^x}{\left(\e^x+1\right)^2} \ `

مشاهدة حل التمرين 2 اغلاق المشاهدة

التمرين 3

` f(x)=\left(x^2+1\right)\e^{2x} و D=R `

أحسب  ` f^'(x)`

` f'(x)=2x\e^{2x}+\left(x^2+1\right)\times 2\e^{2x} \ =\left(2x+2x^2+2\right)\e^{2x} \ =2\left(x^2+x+1\right)\e^{2x} `

مشاهدة حل التمرين 3 اغلاق المشاهدة

التمرين 4

` f(x)=\frac{x^2+\e^x}{4-3x} `

أحسب  ` f^'(x)`

` f'(x)= ` 

`\frac{\left(2x+\e^x\right)(4-3x)-(-3)\left(x^2+\e^x\right)}{(4-3x)^2} =\frac{8x-6x^2+4\e^x-3x\e^x+3x^2+3\e^x}{(4-3x)^2} =\frac{-3x^2+8x+7\e^x-3x\e^x}{(4-3x)^2}`

مشاهدة حل التمرين4 اغلاق المشاهدة

التمرين 5

`f(x) = \sqrt{x^2 + \left(\e^x\right)^2} = \sqrt{x^2 + \e^{2x}} `

` f'(x) = \frac{2x + 2\e^{2x}}{2\sqrt{x^2 + \e^{2x}}} = \frac{x + \e^{2x}}{\sqrt{x^2 + \e^{2x}}} `

مشاهدة حل التمرين 5 اغلاق المشاهدة

التمرين 6

`B(x)=x+4\e^{-x}-5 `

`B'(x)=1+4\times (-1)\e^{-x}=1-4\e^{-x} `

مشاهدة حل التمرين 6 اغلاق المشاهدة

التمرين 7

f(x)=ex+1−−−−−√ I=R

` f'(x)=\frac{e^x}{2\sqrt{e^x+1}} `

مشاهدة حل التمرين 7 اغلاق المشاهدة

التمرين8

` f(x)=3cos(e^x+2) `

` f'(x)=-e^x sin(e^x+2) `

مشاهدة حل التمرين8 اغلاق المشاهدة

التمرين 9

مشاهدة حل التمرين 9 اغلاق المشاهدة

التمرين 10

مشاهدة حل التمرين 10 اغلاق المشاهدة

    ** Ln   مشتق  دالة **

`(Lnf(x))^'=f^'(x)/f(x)`

التمرين11

`  f(x)=Ln(4x+6)`

`   f^'(x)=(4x+6)^'/(4x+6)=4/(4x+6)`

مشاهدة حل التمرين 11اغلاق المشاهدة

التمرين 12

`  f(x)=Ln(2x^2+5x-4)`

`   f^'(x)=(2x^2+5x-4)^'/(2x^2+5x-4)=(4x+5)/(2x^2+5x-4)`

مشاهدة حل التمرين 12 اغلاق المشاهدة

التمرين 13

a. 

b. 

c. 

a.

b.

c.

مشاهدة حل التمرين 13 اغلاق المشاهدة

التمرين 14

 

مشاهدة حل التمرين 14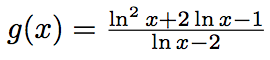اغلاق المشاهدة

التمرين 15

f(x) = ln(x³ - 3x + 1)

` f^'(x)=(3x^2-3)/((x^3-3x+1))`

مشاهدة حل التمرين 15 اغلاق المشاهدة

التمرين 16

`f(x) = \frac{\ln x}{x – \ln x} `

`f'(x) = \frac{\frac{1}{x}(x – \ln x) – \ln x \times \left(1 – \frac{1}{x}\right)}{\left(x – \ln x\right)^2} `

مشاهدة حل التمرين16 اغلاق المشاهدة

التمرين 17

` f(x) = \frac{x}{x + 1} – 2\ln(x + 1) `

` f'(x) = \frac{(x + 1) – x}{(x + 1)^2} – \frac{2}{x + 1} \ =\frac{1}{(x + 1)^2} – \frac{2}{x + 1} \ = \frac{1}{(x + 1)^2} – \frac{2(x+1)}{(x + 1)^2} \ = \frac{-2x – 1}{(x + 1)^2} `

مشاهدة حل التمرين 17 اغلاق المشاهدة

التمرين 18

`g(x) = \frac{\ln(x +1)}{x^2}`

` g'(x) = \frac{\frac{x^2}{x+1} – 2x\ln(x + 1)}{x^4} `

مشاهدة حل التمرين 18 اغلاق المشاهدة

التمرين 19

`f(x) = x(1-\ln x)^2 `

     ` f'(x)=1.\left(1-\ln x\right)^2+x\times \frac{-2}{x}\times \left(1-\ln x\right) \ =\left(1-\ln x\right)\left(\left(1-\ln x\right)-2\right)\ =\left(1-\ln x\right)\left(-1-\ln x\right) \   `

مشاهدة حل التمرين 19 اغلاق المشاهدة

**الدالنين exp و ln**

التمرين 20

`f(x)=\left(x^3-2x^2\right)\e^x`

` f'(x)=\left(3x^2-4x\right)\e^x+\left(x^3-2x^2\right)\e^x \ =\left(3x^2-4x+x^3-2x^2\right)\e^x \ =\left(x^3+x^2-4x\right)\e^x \ =x\left(x^2+x-4\right)\e^x `

مشاهدة حل التمرين 20 اغلاق المشاهدة

التمرين 21

`f(x)=\frac{4-\e^x}{1-x} `

` f'(x)=\frac{-\e^x\times (1-x)-(-1)\times \left(4-\e^x\right)}{(1-x)^2} \ =\frac{-\e^x+x\e^x+4-\e^x}{(1-x)^2} \ =\frac{x\e^x-2\e^x+4}{(1-x)^2} `

مشاهدة حل التمرين 21 اغلاق المشاهدة

التمرين 22

`f(x)=\frac{x^2+\e^x}{4-3x} `

` f'(x)=\frac{\left(2x+\e^x\right)(4-3x)-(-3)\left(x^2+\e^x\right)}{(4-3x)^2} \ =\frac{8x-6x^2+4\e^x-3x\e^x+3x^2+3\e^x}{(4-3x)^2} \ =\frac{-3x^2+8x+7\e^x-3x\e^x}{(4-3x)^2} `

مشاهدة حل التمرين 22 اغلاق المشاهدة

التمرين 23

`f(x)=x^2\ln x `

` f'(x)=2x\ln x+x^2\times \frac{1}{x} \ =2x\ln x+x \ =x(2\ln x+1) `

مشاهدة حل التمرين 23 اغلاق المشاهدة

التمرين 24

`g(x)=x\ln x-2x `

` g'(x)=1.\ln x+x\times \frac{1}{x}-2\ =\ln x+1-2 \ =\ln x-1 `

مشاهدة حل التمرين 24 اغلاق المشاهدة

التمرين 25

`f(x) = \frac{\ln x}{x – \ln x} `

`f'(x) = \frac{\frac{1}{x}(x – \ln x) – \ln x \times \left(1 – \frac{1}{x}\right)}{\left(x – \ln x\right)^2}= \frac{1 – \ln x}{\left(x – \ln x\right)^2} `

مشاهدة حل التمرين 25 اغلاق المشاهدة

التمرين 26

`f(x)=3x\ln x-9x+10 `

`f'(x)=3\times \ln x+3x\times\frac{1}{x}-9\ =3\ln x+3-9\ =3\ln x-6 `

مشاهدة حل التمرين 26 اغلاق المشاهدة

التمرين 27

`f(x) = (x+1)\e^{-2x + 3} `

` f'(x)=\e^{-2x+3}-2(x+1)\e^{-2x+3} \ =(1-2x-2)\e^{-2x+3} \ =(-1-2x)\e^{-2x+3} `

مشاهدة حل التمرين 27 اغلاق المشاهدة

التمرين 28

`f(x)=\frac{5+5\ln(x)}{x} `

` f'(x)=\frac{-5\ln x}{x^2} `

مشاهدة حل التمرين 28 اغلاق المشاهدة

التمرين30

`f(x)=x^2(1-\ln x) `

` f'(x)=2x(1-\ln x)-x^2\times \frac{1}{x} \ =2x-2x\ln x-x\ =x-2x\ln x \ =x(1-2\ln x) `

مشاهدة حل التمرين 30 اغلاق المشاهدة

**تمارين متنوعة**

التمرين الاول

اليك التمثيل البياني لدالة كماهو موضح 

ماهو عدد حلول المعادلة ` f^'(x)=0`

ماهي اشارة العدد        `f^'(7)`

المعادلة تقبل حليين لانها تغيير اتجاهها مرتتن عند x=0.5 ;x=5.5 على مجموعة تعريفها

الدالة متناقصة على المجال [5,5;10] وعليه f'(7)<0

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الاول

صح أوخطأ مع التعليل

1)  ` f^'(0)=1`   

  2)  `f^'(-1)=0`  

 3) `f^'(-3)=-1`  

4) `f^'(-3)=3`   

1) خطأ لان المما س عند 0 يوازي الفواصل  ومنه ` f^'(0)=0`

2) المنحنى لا يقبل عند -1 مماس موازي للفواصل   ومنه  خطأ

3) الدالة متناقصة لما x く0  ومنه `f^'(-3)く0`  صح

3) الدالة متناقصة لما x く0  ومنه `f^'(-3)く0`  خطأ

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الاول

وضع التمرين الاول

حل التمرين الاول

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الاول

وضع التمرين الاول

حل التمرين الاول

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الاول

وضع التمرين الاول

حل التمرين الاول

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الاول

وضع التمرين الاول

حل التمرين الاول

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الاول

وضع التمرين الاول

حل التمرين الاول

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الاول

وضع التمرين الاول

حل التمرين الاول

مشاهدة حل التمرين الاول اغلاق المشاهدة

التمرين الاول

وضع التمرين الاول

حل التمرين الاول

مشاهدة حل التمرين الاول اغلاق المشاهدة

`*`